At the Open Source Bridge hacker lounge, Ward Cunningham was talking about borrowing a Mac Mini to run his
Txtzyme Sparkles at an art show.
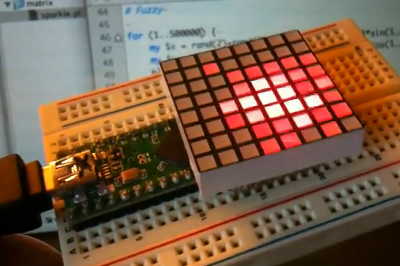
Rather than go home at a reasonable hour, I thought it'd be fun to try implementing all the math directly on the Teensy++, using only the Arduino IDE. Making it run was easy, but doing the math as fast as the computer+USB was quite a challenge.
"Read more" for the stand alone Arduino-based code.... which can run as fast, even faster than the USB communication allows.
Here is Ward's Perl code, which this little hack tries to replicate directly on Teensy++ (only a 16 MHz 8 bit processor)
This first attempt, using floating point numbers as Perl does, with nearly identical math simply converted to Arduino worked.... SLOWLY. It was very slow indeed, but converting the code only took maybe 15 or 20 minutes.
void setup() {
}
float rn(void) {
long r = random(0, 200000) + random(0, 200000) +
random(0, 200000) + random(0, 200000);
return r * 0.00001;
}
byte anode[] = {42, 15, 14, 39, 12, 40, 44, 45};
byte cathode[] = {38, 43, 10, 41, 17, 11, 16, 13};
char x=0, y=0;
void loop() {
static float t=0;
if (x >= 0 && x <= 7 && y >= 0 && y <= 7) {
digitalWrite(anode[x], HIGH);
pinMode(anode[x], OUTPUT);
digitalWrite(cathode[y], LOW);
pinMode(cathode[y], OUTPUT);
delayMicroseconds(50);
char xold = x;
char yold = y;
pinMode(anode[xold], INPUT);
pinMode(cathode[yold], INPUT);
x = rn() + 3.0 * sin(7.7 * t);
y = rn() + 3.0 * cos(3.1 * t);
} else {
x = rn() + 3.0 * sin(7.7 * t);
y = rn() + 3.0 * cos(3.1 * t);
}
t = t + 0.0002;
}
Throughout the evening, I tried many ideas and eventually replaced all the floating point math with 32 bit integers. Ward suggested using a short loopup table for the sine/cosine, since it only needs to be accurate to a little over 3 bits to determine which of the 8 rows or columns to light.
Eliminating the floats helped, but it was still far too slow. After much experimentation, it turned out the random number function from Arduino was very slow, and it was being called 4 times to get a nice distribution. Ward suggested just using a lookup table there too. It turns out that code does a 32 bit modulus operation internally, which is slow looped code within the C library. Progress.
Now it was almost as fast, but still not quite there. Here's the fixed point code with tables for sine/cosine and random.
char sn[128];
const int nrnd=333;
byte rnd[nrnd];
void setup() {
for (int i; i<128; i++) {
sn[i] = 96*sin(i*2*3.14159/128);
}
for (int i; i<nrnd; i++) {
rnd[i] = rn();
}
}
int rn(void) {
int r = random() & 0xFF;
r += random() & 0xFF;
r += random() & 0xFF;
r += random() & 0xFF;
return r >> 2;
}
byte anode[] = {42, 15, 14, 39, 12, 40, 44, 45};
byte cathode[] = {38, 43, 10, 41, 17, 11, 16, 13};
char x=0, y=0;
void loop() {
static unsigned long i1=0, i2=0;
static unsigned int rindex=0;
if (x >= 0 && x <= 7 && y >= 0 && y <= 7) {
digitalWrite(anode[x], HIGH);
pinMode(anode[x], OUTPUT);
digitalWrite(cathode[y], LOW);
pinMode(cathode[y], OUTPUT);
delayMicroseconds(50);
char xold = x;
char yold = y;
x = (rnd[rindex] + sn[i1>>25]) >> 5;
pinMode(anode[xold], INPUT);
pinMode(cathode[yold], INPUT);
y = (rnd[rindex+1] + sn[((i2>>25)+32)&127]) >> 5;
} else {
x = (rnd[rindex] + sn[i1>>25]) >> 5;
y = (rnd[rindex+1] + sn[((i2>>25)+32)&127]) >> 5;
}
i1 = i1 + 526335;
i2 = i2 + 211913;
rindex = rindex + 1;
if (rindex >= nrnd - 2) rindex = 0;
}
The final bit of slowness, after much more hacking, turned out to be the right shift by 25 bits.
In the float to integer conversion, I replaced the float with a 32 bit long, and intead of incrementing the float by 0.0002, I incremented two separate integers by 526335 and 211913. That caused the top 7 bits to sweep exactly once through the table for the same number of iterations of the loop as the float code would sweep from 0 to 2*pi. The 32 bit number would overflow back to 0 exactly as the original code became 6.2831853 (each integrating the 7.7 and 3.1 scale factors into the integer addition), which perfectly leveraged integer overflow. Crafty, but still too slow!!
It turned out the compiler was using a slow loop to implement the 25 bit right shift. I changed it to 24 bits, by adding half as much each time through the loop. After a quick fix to mask off the top bit, for 31 bit integer overflow, suddenly the Arduino-based code could run MUCH FASTER than Txtzyme could receive and process commands from the Mac.
Along the way, I also removed the pinMode and digitalWrite and replaced them with case statements. That runs faster, but only a tiny increase.
With all the optimizations in place, Ward and I spent a little time (as midnight approached) tweaking at extra delayMicroseconds() to make the stand-alone version closely match the speed of Txtyzme with the Perl script. Here is that final "same speed" code, with the 72 us delay.
char sn[128];
const int nrnd=333;
byte rnd[nrnd];
void setup() {
for (int i; i<128; i++) {
sn[i] = 96*sin(i*2*3.14159/128);
}
for (int i; i<nrnd; i++) {
rnd[i] = rn();
}
}
int rn(void) {
int r = random() & 0xFF;
r += random() & 0xFF;
r += random() & 0xFF;
r += random() & 0xFF;
return r >> 2;
}
byte anode[] = {42, 15, 14, 39, 12, 40, 44, 45};
byte cathode[] = {38, 43, 10, 41, 17, 11, 16, 13};
char x=0, y=0;
void loop() {
static unsigned long i1=0, i2=0;
static unsigned int rindex=0;
if (x >= 0 && x <= 7 && y >= 0 && y <= 7) {
switch(x) {
case 0: PORTF |= (1<<4); DDRF |= (1<<4); break;
case 1: PORTC |= (1<<5); DDRC |= (1<<5); break;
case 2: PORTC |= (1<<4); DDRC |= (1<<4); break;
case 3: PORTF |= (1<<1); DDRF |= (1<<1); break;
case 4: PORTC |= (1<<2); DDRC |= (1<<2); break;
case 5: PORTF |= (1<<2); DDRF |= (1<<2); break;
case 6: PORTF |= (1<<6); DDRF |= (1<<6); break;
case 7: PORTF |= (1<<7); DDRF |= (1<<7); break;
}
//digitalWrite(anode[x], HIGH);
//pinMode(anode[x], OUTPUT);
switch(y) {
case 0: PORTF &= ~(1<<0); DDRF |= (1<<0); break;
case 1: PORTF &= ~(1<<5); DDRF |= (1<<5); break;
case 2: PORTC &= ~(1<<0); DDRC |= (1<<0); break;
case 3: PORTF &= ~(1<<3); DDRF |= (1<<3); break;
case 4: PORTC &= ~(1<<7); DDRC |= (1<<7); break;
case 5: PORTC &= ~(1<<1); DDRC |= (1<<1); break;
case 6: PORTC &= ~(1<<6); DDRC |= (1<<6); break;
case 7: PORTC &= ~(1<<3); DDRC |= (1<<3); break;
}
//digitalWrite(cathode[y], LOW);
//pinMode(cathode[y], OUTPUT);
delayMicroseconds(50);
char xold = x;
char yold = y;
switch(xold) {
case 0: PORTF &= ~(1<<4); DDRF &= ~(1<<4); break;
case 1: PORTC &= ~(1<<5); DDRC &= ~(1<<5); break;
case 2: PORTC &= ~(1<<4); DDRC &= ~(1<<4); break;
case 3: PORTF &= ~(1<<1); DDRF &= ~(1<<1); break;
case 4: PORTC &= ~(1<<2); DDRC &= ~(1<<2); break;
case 5: PORTF &= ~(1<<2); DDRF &= ~(1<<2); break;
case 6: PORTF &= ~(1<<6); DDRF &= ~(1<<6); break;
case 7: PORTF &= ~(1<<7); DDRF &= ~(1<<7); break;
}
//pinMode(anode[xold], INPUT);
switch(yold) {
case 0: PORTF &= ~(1<<0); DDRF &= ~(1<<0); break;
case 1: PORTF &= ~(1<<5); DDRF &= ~(1<<5); break;
case 2: PORTC &= ~(1<<0); DDRC &= ~(1<<0); break;
case 3: PORTF &= ~(1<<3); DDRF &= ~(1<<3); break;
case 4: PORTC &= ~(1<<7); DDRC &= ~(1<<7); break;
case 5: PORTC &= ~(1<<1); DDRC &= ~(1<<1); break;
case 6: PORTC &= ~(1<<6); DDRC &= ~(1<<6); break;
case 7: PORTC &= ~(1<<3); DDRC &= ~(1<<3); break;
}
//pinMode(cathode[yold], INPUT);
x = (rnd[rindex] + sn[(i1>>24)&127]) >> 5;
y = (rnd[rindex+1] + sn[((i2>>24)+32)&127]) >> 5;
} else {
x = (rnd[rindex] + sn[(i1>>24)&127]) >> 5;
y = (rnd[rindex+1] + sn[((i2>>24)+32)&127]) >> 5;
}
i1 = i1 + (526335/2);
i2 = i2 + (211913/2);
rindex = rindex + 1;
if (rindex >= nrnd - 2) rindex = 0;
delayMicroseconds(72);
}
So there it is, right at the end, an extra 72 us delay needed to match the original speed....
Of course, this was pretty difficult to optimize for speed, and that was with the Txtyzme version already fully developed. The ease to just editing a tiny bit of Perl and getting a dramatically different display is pretty amazing.
There were also some slight visual artifacts, probably from using the lookup tables. A big improvement, which wouldn't take much CPU time, would involve getting the 2 sets of random numbers from the table by incrementing different number of positions in the table, maybe 2 different prime numbers? Or longer tables could be used, since there's lots of unused RAM, and they could be put in flash using PROGMEM.
But this was really just quick hacking, late at the Open Source Bridge hacker lounge... all done from about 9pm to midnight on the open Tuesday session. I'm not sure if Ward is planning to use this or write any more about it (or make videos comparing them??), or really if anyone might ever find this optimization stuff interesting, but there is it anyway.